最近的工作中遇到两个常见的运动学相关的问题，下文就这两个问题分享一下我个人的浅见，希望能抛砖引玉。

问题一：抛物线解算

抛物线运动在游戏开发中，特别是在考虑重力的前提下，是一种很常见的运动形式。

然而相比直线运动而言，想要解出抛物线运动的初速度和时间似乎并不是那么直观，但其实只要正确地将抛物线运动进行分解，求解上述变量几乎是易如反掌。

问题定义

给定起点$A$，终点$B$，重力加速度$g$，抛物线最高点与$A$或$B$之间的竖直距离$h$，计算物体从$A$运动到$B$的初速度和时间

注意：为了保证问题一定有解，这里将抛物线的最高点$y_{max}$定义为：$A$和$B$中较高的一个的竖直坐标$+h$，即$y_{max} = Max(A.y, B.y) + h$

求解原则

开始求解之前，我们有必要了解一下抛物线问题的几个特点

1. 抛物线运动可以拆分为水平方向和竖直方向两个子方向上的运动。三维情况下则可以拆分为平面方向和竖直方向；
2. 水平方向的运动为匀速直线运动，竖直方向的运动为匀加速直线运动，假设加速度为$g$；
3. 竖直方向上的运动可以进一步分解为上升和下降两个阶段；
4. 水平方向与竖直方向的运动时间相同；
5. 匀加速直线运动一共有5个基本变量，位移$s$，时间$t$，加速度$a$，初速度$v_0$，末速度$v_t$，利用公式，已知其中三个就可以求出余下的两个；
6. 匀加速直线运动一共有5个基本公式，每个公式中分别缺少1个基本变量
   1. $v_t = v_0 + at$
   2. $s = v_0t + \frac{at^2}{2}$
   3. $s = v_tt – \frac{at^2}{2}$
   4. $s = (v_o + v_t)/2 *t$
   5. $2as = v_t^2 – v_0^2$
      （我自己对公式5已经没什么记忆了，但只要将公式1变形得到$t$后代入公式4，即可得到公式5）

求解步骤

上升阶段：匀加速直线运动

• 已知：加速度$g$，末速度$v_{t\_up}=0$，位移$s_{up}=y_{max}-A.y$
• 可求：初速度$v_{0\_up}$，时间$t_{up}$

下降阶段：匀加速直线运动

• 已知：加速度$g$，初速度$v_{0\_down}$=0，位移$s_{down} = y_{max}-B.y$
• 可求：时间$t_{down}$，末速度$v_{t\_down}$

水平运动：匀速直线运动

• 已知：时间$t_{plane} = t_{up} + t_{down}$，位移 $A_{plane} – B_{plane}$ （即A和B在y=0平面投影间的距离）
• 可求：速度$v_{plane}$

求解全程只需要套用对应的公式即可，这里不再赘述。

有了以上计算结果，最终可以计算物体的初速度：$v_{init} = v_{0\_up} + v_{plane}$，和运动时间：$t_{sum} = t_{plane} = t_{up} + t_{down}$

位置解算

若物体按上述初速度运动，则物体在任意时刻$t$的位置可以表示为：$$p_t = A + v_{init} * t – \frac{gt^2}{2} (g > 0)$$

结果验证

在Unity中新建一个场景，放入两个刚体小球A和B，并新建一个脚本。

脚本在检测到玩家输入后，需要计算并给小球$A$施加一个能按抛物线运动到$B$的初速度，如果最终小球$A$可以命中小球$B$，则说明计算正确

关键代码

public static LaunchData CalcLaunchData(Vector3 sourcePos, Vector3 targetPos, float h, float g)  
{  
    var highestY = Mathf.Max(sourcePos.y, targetPos.y) + h;  
    var displacementUp = highestY - sourcePos.y;  
    var displacementDown = highestY - targetPos.y;  
    var velocityUp = Mathf.Sqrt(-2 * g * displacementUp) * Vector3.up;  
    var timeUp = velocityUp.y / -g;  
    var timeDown =  Mathf.Sqrt(-2 * displacementDown / g);  
    var displacementPlane = new Vector3((targetPos - sourcePos).x, 0, (targetPos - sourcePos).z);  
    var velocityPlane = displacementPlane / (timeUp + timeDown);  
    LaunchData launchData;  
    launchData.SumTime = timeUp + timeDown;  
    launchData.InitialVelocity = velocityUp + velocityPlane;  
    return launchData;  
}

运行结果

另一种方案

贝塞尔曲线也是一个可以考虑的解决方案，它可以脱离任何运动学知识，直接模拟出一条曲线运动轨迹

但使用贝塞尔曲线需要满足以下几个条件

• 可以在运动过程中实时改变物体的速度
• 可以忽略重力
• Tick频率固定
• 对轨迹没有特殊要求（仅希望是曲线，但对h不作要求）

总的来说，虽然使用贝塞尔曲线相对简单，但它本质上并不能解答上文定义的问题，且它的可控性不如运动学结算出的抛物线，因为我们只是每帧从曲线上采样，然后让物体运动到采样点。

我们以最简单的二次贝塞尔曲线为例，其曲线上的点可以表示为：$$P_t = (1-t)^2 A + 2t(1-t) * P_{ctrl} + t^2B (t \in [0, 1])$$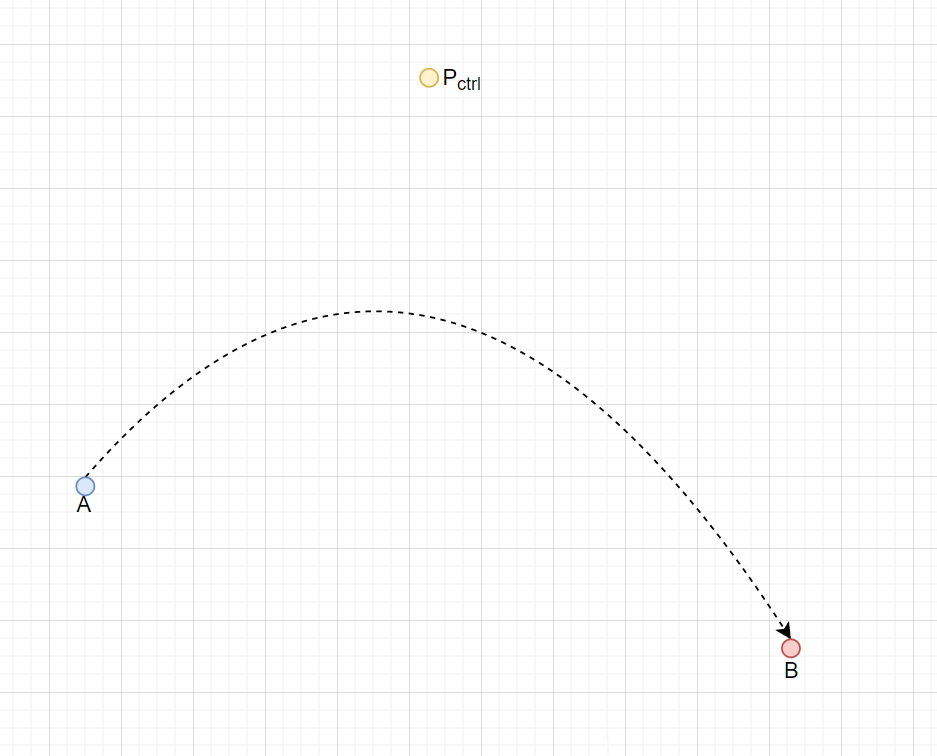

要使用二次贝塞尔曲线，我们需要

1. 运动前在$A$和$B$之间找一个合适的控制点$P_{ctrl}$，但要注意曲线并不会经过这个点
2. 之后在每帧Tick时，我们将归一化后的时刻$t$（当前已运动时间 / 拟运动总时间）代入公式，求出该时刻对应的曲线点
3. 反推出物体运动到曲线点的速度大小和方向，并施加给物体。

问题二：动态目标追踪

接下来我们尝试让目标B运动起来，然后在不考虑其他外力（如重力）的情形下，让$A$以某一大小固定的速度持续追踪目标$B$，模拟”跟踪导弹“的运动效果。

问题定义

每帧给定导弹$A$的位置和飞行速度大小$v_A$、目标$B$的位置和速度大小$v_B$及方向$dir_B$，计算为使导弹$A$尽早命中目标$B$，$A$本帧的运动速度方向$dir_A$

朴素追踪

一个最直接的解法是，每帧设置$A$向$B$当前的位置运动，即$dir_A = \overrightarrow{AB} / |{\overrightarrow{AB}}|$。

private void PureTracking()  
{  
    TrackingImpl(sphereTarget.transform.position);  
}

这种方法虽然简单，但缺点也很明显：

• 没有使用$B$的速度来对$B$的位置进行预测，导致追踪路径和时间较长。
• 在将要命中$B$前的一段时间，$A$的运动方向可能会出现较大偏转，导致运动轨迹中有较为陡峭的转角

朴素追踪+预测

为了对$B$的位置进行一定程度的预测，我们可以假设$B$之后的运动是匀速直线运动，然后尝试追踪$t$时间之后$B$的位置$B’$：$$B’ = B + t * v_B * dir_B*$$
但是当$A$和$B$的位置接近时，如果我们仍然追踪$t$时间之后的位置，则大概率会无法命中。因此更一般地，$t$应该随着$AB$距离的减小而减小，且应该有合理的上下限

使用插值和反向插值，可以轻松实现两个区间的映射：

private void PredictTracking()  
{  
    var leadTimePercentage = Mathf.InverseLerp(minPredictionDis, maxPredictionDis, Vector3.Distance(cubeTracker.transform.position, sphereTarget.transform.position));  
    var predictionTime = Mathf.Lerp(0, maxPredictionTime, leadTimePercentage);  
    var predictedTrackingPos = sphereTarget.transform.position + predictionTime * sphereTarget.velocity;  
    TrackingImpl(predictedTrackingPos);
}

其中，minPredictionDis和maxPredictionDis分别表示距离区间的上下限，将$AB$距离反向插值后可以得到一个0到1之间的距离比例leadTimePercentage，之后再将该比例映射回预测时间区间，即可得到最终的预测时间$t$，进而算出当前帧的追踪点$B’$和导弹的速度方向$dir_A$。

拦截追踪

既然我们可以预测匀速直线运动时，$B$在未来的位置，那么能否更进一步，直接求出$A$命中$B$时的位置呢（显然$A$运动到该位置的时间等于$B$运动到该位置的时间）？答案是肯定的。

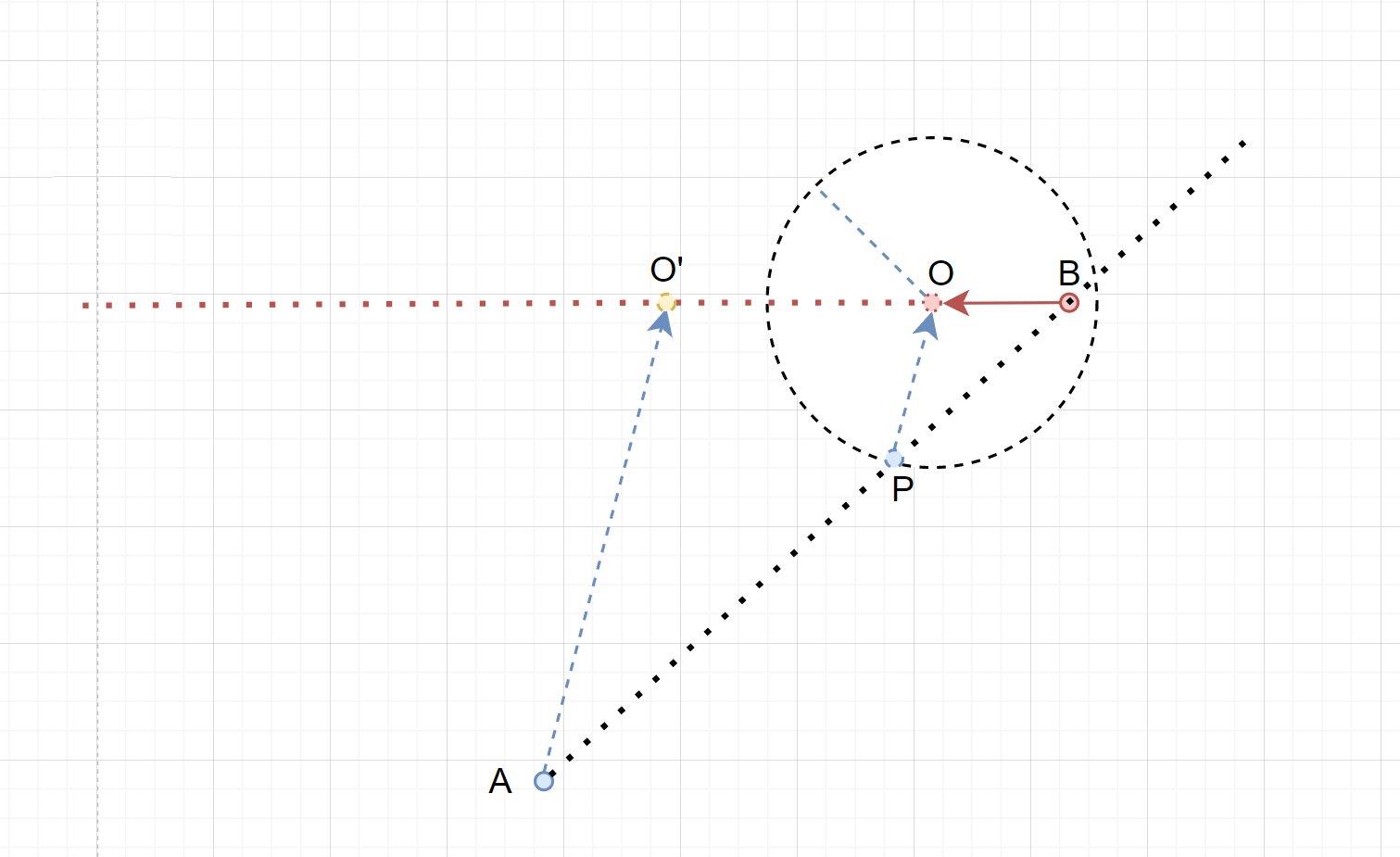
以上图为例，假设当前帧下，$A$和$B$的位置分别位于点$A$和点$B$，$\overrightarrow{BO}$是$B$的运动速度矢量。

以$O$为球心，$A$的运动速度大小$v_A$为半径画球，假设该球与直线$AB$相交于点$P$（后面会讨论交点的有效性、第二个交点和没有交点的情况），则$\overrightarrow{PO}$就是$A$拦截$B$的运动方向$dir_A$。

证明

过$A$做一条平行于$PO$的辅助线，与$BO$相交于$O’$，显然$\triangle BOP$ 和 $\triangle BO’A$是相似三角形，因此对应边成比例。

$B$经过单位时间t会运动到点$O$，如果此前点$A$也正好位于点$P$，则$A$同样可以经过单位时间$t$运动到点$O$，即A命中B，因为$|\overrightarrow{PO}| = v_A$。

因此，如果$B$经过时间$t’$可以运动到$O’$，则$A$同样可以经过时间$t’$运动到$O’$，因为$BO / BO’ = PO / AO’$。所以如果$B$接下来的运动速度保持不变，则$A$可以沿$|\overrightarrow{PO}|$方向作匀速直线运动，并最终命中$B$。

其他情况

上述讨论只是诸多情况中的一种，并不充分。

实际上，球与直线$AB$求交，本身就可能出现三种情况：没有交点、一个交点、两个交点，而交点又可能与点A和点B组成不同的相对位置关系。下图对各种不同情况进行了展示：

其中，

• (a)：$\angle ABO$为锐角，导弹$A$的速度大小$a$大于等于目标$B$的速度$b$（$a >= b$），=> 2个交点，交点$P’$无效
• (b)：$\angle ABO$为锐角，$b * \sin(\angle ABO) < a < b$， => 2个交点，都有效（$b * \sin(\angle ABO)$为球心$O$到直线$AB$的距离）
• (c)：$\angle ABO$为锐角，$a = b * \sin(\angle ABO)$， => 1个交点，有效
• (d)：$\angle ABO$为锐角，$a < b * \sin(\angle ABO)$， => 没有交点
• (e)：$\angle ABO$为钝角，$a > b$，=> 2个交点，交点$P’$无效
• (f)：$\angle ABO$为钝角，$a <= b$，=> 依然可能有2个、1个或0个交点，但交点都在$B$的上方，均无效

根据上述讨论我们可以得出：

1. 直线与球有交点时不代表一定有解，但没有交点时一定无解
2. 有交点时，符合物理规律的交点一定与$A$一起，在$B$的同侧，即$|AP| + |PB| = |AB|$
3. 交点与$B$重合时也不算有效
4. 有时可能同时存在两个有效解，代表有两种拦截方式

实现

代码实现的核心主要是求解直线$AB$和球$O$的交点。直线方程最好使用点向式：$$P = A + \alpha*\overrightarrow{AB}$$
其中$P$表示直线上的某点，$\alpha$是该点对应的参数。使用$\overrightarrow{AB}$作为方向向量的好处是，对于有效的交点$P$而言，其$\alpha$值一定小于1（可以小于0）

将上述式子拆分后，可以得到每个子坐标的表达式：
$$
\left{
\begin{array}{l}
P_x = A_x + \alpha * \overrightarrow{AB}_x \
P_y = A_y + \alpha * \overrightarrow{AB}_y \
P_z = A_z + \alpha * \overrightarrow{AB}_z
\end{array}
\right.
$$

而球的方程可以直接使用定义 $$(P_x – O_x)^2 + (P_y – O_y)^2 + (P_z – O_z)^2 = R^2$$
之后将前3个公式代入第4个，可以得到一个关于$\alpha$的一元二次方程，使用求根公式解出$\alpha$即可。一个值得注意的点是，根据我们之前的分析，如果存在有效解，那么更小的那个根一定是有效的。

将上述计算转换为代码就是：

private void LeadTracking()  
{  
    var trackerPosition = cubeTracker.transform.position;  
    var targetPosition = sphereTarget.transform.position;  
    var trackingMotion = targetPosition - trackerPosition;  
    var AB = trackingMotion;  
    var A = trackerPosition;  
    var O = targetPosition + sphereTarget.velocity;  
    var R = trackerSpeed;  
  
    var a = AB.x * AB.x + AB.y * AB.y + AB.z * AB.z;  
    var b = 2 * (AB.x * (A.x - O.x) + AB.y * (A.y - O.y) + AB.z * (A.z - O.z));  
    var c = (A.x - O.x) * (A.x - O.x) + (A.y - O.y) * (A.y - O.y) + (A.z - O.z) * (A.z - O.z) - R * R;  
    var delta = b * b - 4 * a * c;  
  
    if (delta >= 0)  
    {
	var alpha = (-b - Mathf.Sqrt(delta)) / 2.0f / a;  
        if (alpha < 1)  
        {
	    var leadOffset = sphereTarget.velocity / (1-alpha);  
            TrackingImpl(targetPosition + leadOffset);  
            return;  
        }    
    }
    TrackingImpl(targetPosition);  
}

另一种证明&实现

文章发布后，@ivenszhao(赵志翔) 同学提供了一种新的推导和实现方法，这里也尝试理解和记录一下。

使用相对运动推导

首先是如何利用“相对运动”的概念来推出导弹追踪的方向。假设目标B的运动矢量为$v_B$，那么若以$B$为参考系，则$B$静止不动，其他物体的运动矢量均为$-v_B$。此时如果导弹$A$希望命中目标$B$，则问题变为：在已有一个$-v_B$的运动分量的前提下，如何叠加一个新的分量$v_A$，使$A$最终沿$\overrightarrow {AB}$方向运动。

如上图所示，以$O’$为球心，$v_A$大小为半径做球，球心到球面上各点的向量就是$A$最终可能的运动矢量。假设球与直线$AB$相交与点$P$，则$\overrightarrow {O’P}$（即$v_A’$）就是要叠加的新的运动分量，而$\overrightarrow{AP}$就是$A$最终相对于$B$的运动矢量。

不难证明，这里推导出的$v_A’$与之前推导出的$v_A$是相同的向量。而如果要计算碰撞点，可以通过$|\overrightarrow{AP}|$与$|\overrightarrow{AB}|$的比例求出运动时间，再乘以$A$或$B$的速度即可。

通过解三角形计算交点

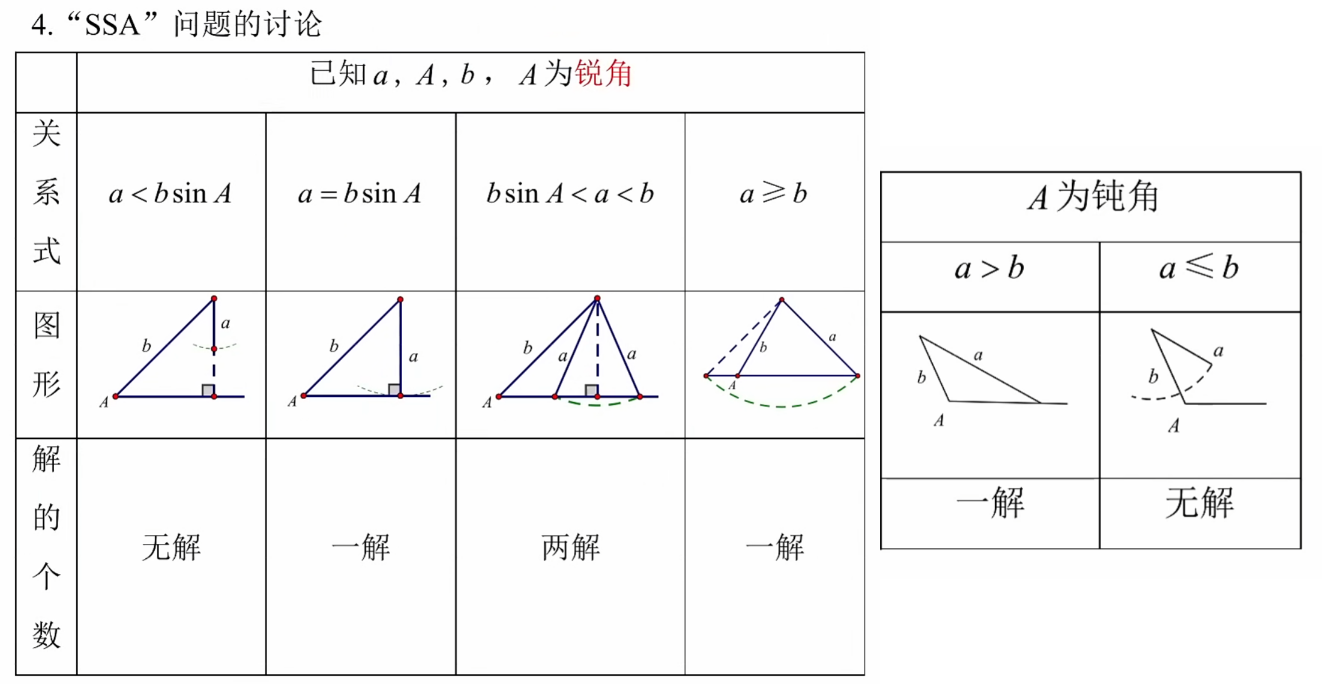
上文中我们比较直观地使用球与直线相交和一元二次方程计算出碰撞位置，ivens指出还可以使用“解三角形”的思路来完成求解。

还以上图为例，$AO’$、$O’P$、$\angle PAO’$ 都是已知条件（“边边角”，SSA），我们可以使用正弦定理来计算出边$AP$的长度，进而得到点P。但要注意的是，“边边角”并不能完全确定一个三角形，与解一元二次方程类似，这里我们仍然需要讨论无解和多解的情况，如下图所示：

具体如何套用到本问题中这里不再赘述，原则上需要仔细考察每种情况和三角函数、反三角函数的输入输出范围，代码如下：

private void LeadTracking2()  
{  
    var trackingMotion = sphereTarget.transform.position - cubeTracker.transform.position;  
    var targetVelocity = sphereTarget.velocity;  
    var sideA = trackerSpeed;  
    var sideB = targetVelocity.magnitude;  
    var cosAngleA = -Vector3.Dot(trackingMotion, targetVelocity) / trackingMotion.magnitude / sideB;  
    var sinAngleA = Mathf.Sqrt(1 - cosAngleA * cosAngleA);  
    var sinAngleB = sideB * sinAngleA / sideA;  
    var hasValidSln = false;   
    if (cosAngleA > 0)  // A为锐角  
    {  
        if (sideA >= sideB * sinAngleA)  
        {  
            hasValidSln = true;  
        }  
    }  
    else  // A为直角或钝角  
    {  
        if (sideA > sideB)  
        {  
            hasValidSln = true;  
        }  
    }  

    if (hasValidSln)  
    {  
        var cosAngleB = Mathf.Sqrt(1 - sinAngleB * sinAngleB);  
        var sinAngleC = sinAngleA * cosAngleB + cosAngleA * sinAngleB;  
        var sideC = sideB * sinAngleC / sinAngleB;  
        var trackingPos = sphereTarget.transform.position + (trackingMotion.magnitude / sideC) * sphereTarget.velocity;  
        TrackingImpl(trackingPos);  
    }  
    else  
    {  
        TrackingImpl(sphereTarget.transform.position);  
    }  
}

Asin() > Sin() > Sqrt()

根据ivans的评论，自己对不同实现方式进行了一个简单的profile，从结果中可以看出三者的耗时关系大致为“反三角函数>三角函数>平方根函数”。所以如果仔细阅读上面的代码就会发现，里面优化掉了所有的三角函数和反三角函数。

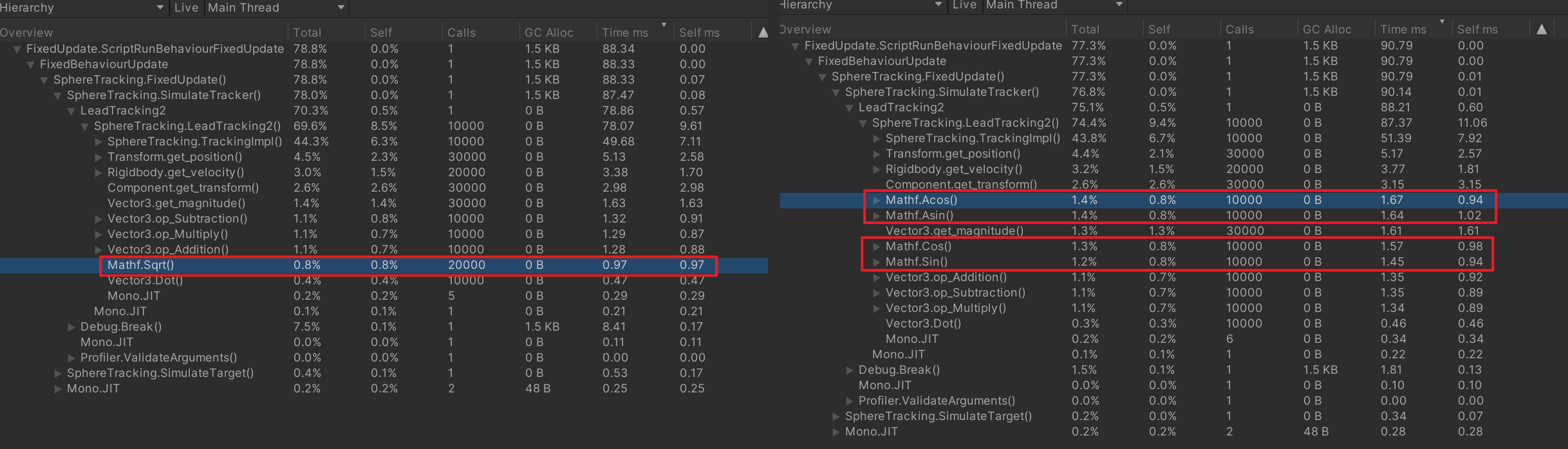
同理，使用解一元二次方程的方式计算结果，仅会用到平方根函数，耗时也会比使用三角函数更少。

结果验证&分析

我们继续沿用抛物线时的场景进行验证，但为了表现导弹的旋转，这里用Cube替换了之前的Sphere，之后分别用上文的三种方法来进行追踪测试。

实验结果显示，在A和B都做匀速直线运动的相同条件下，三种追踪算法的追踪时间依次为：4.07s、3.73s、3.59s，可以看出拦截算法在目标物体速度大小和方向变化平缓时的优势

但当目标物体的运动速度可能发生剧烈变化时，拦截追踪算法反而会因为预测位置的骤变而适得其反，导致追踪时间变长（下面的视频中追踪用时为5.60s）：

而“朴素追踪”和“朴素追踪+预测”的方法由于没有预测或对预测时间进行了限制，因此依然能够正常追踪到目标，追踪时间分别为5.42s和5.25s。下面两个视频为“朴素追踪”和“朴素追踪+预测”的表现：

因此在游戏开发中，如果想模拟”跟踪导弹“的效果，除了直接追踪目标物体的位置外，还可以根据目标物体的速度加入适当的预测。如果想进一步引入一些多样性和随机性，还可以参考“How to make a Homing Missile in Unity with Trajectory Prediction”，引入一定的预测偏差。而如果目标物体的移动速度的大小和方向变化比较平缓，还可以考虑使用拦截算法，来让导弹更快地命中目标。

Reference

1. 【匀变速直线运动】公式推导_哔哩哔哩_bilibili
2. Kinematic Equations (E03: ball problem) – YouTube
3. How to make a Homing Missile in Unity with Trajectory Prediction (source included) – YouTube
4. Homing missile lead collision algorithm tutorial – YouTube
5. 空间直线与球面相交算法 – charlee44 – 博客园
6. [高一数学寒假3]正弦定理初步＆解三角形多解问题讨论_哔哩哔哩_bilibili